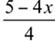Discussion
If x ≠ 3/4, which one of the following will equal −2 when multiplied by 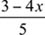 ?
?
| (A) |
|
| (B) | ... |
| (C) | ... |
| (D) | ... |
| (E) | ... |
| (F) | ... |
The solution is
Posted: 11/30/2012 18:06
I understand the algebra part of this question, but I don't understand how we know x=0 if they simply say it is not 3/4?
Posted: 12/01/2012 05:08
Erica,
That you get a range in a domain where the function applies is normal.
Particular with rational expressions you'll get the x is not, this is more often seen when x is in the denominator since the denominator can't be 0.
This to say x is not (3/4) has no meaning to us at this point.
I would solve the exercise like this:
((3-4x)/5) * ? = -2
A * B = C
C / A = B
(-2/1) / ((3-4x)/5) = B
(-2/1) * (5/(3-4x)) = B
-10/(3-4x) = B
10/(-3+4x) = B
10/(4x-3) = B
Niels
That you get a range in a domain where the function applies is normal.
Particular with rational expressions you'll get the x is not, this is more often seen when x is in the denominator since the denominator can't be 0.
This to say x is not (3/4) has no meaning to us at this point.
I would solve the exercise like this:
((3-4x)/5) * ? = -2
A * B = C
C / A = B
(-2/1) / ((3-4x)/5) = B
(-2/1) * (5/(3-4x)) = B
-10/(3-4x) = B
10/(-3+4x) = B
10/(4x-3) = B
Niels
Posted: 12/01/2012 16:33
Erica,
You are probably more interested in the answer to the x=0 mystery :)
If x cannot be (3/4) then it can be 0, it can also be 2, 3 or (13/2)
WE NEED an actual value for x to calculate the expression.
The solution given in the app takes x=0 but we can take 'every' number for x BUT (3/4).
You already might have noticed that when x is allowed to be 0, often the 0 is taken above all other numbers because 0 will lessen the calculations ergo 20x >>> 20*23 against 20*0, which would you prefer :)
we'll take x = 2
((3 - 4x) / 5) * (10 / (4x - 3)) = -2
((3 - 4(2)) / 5) * (10 / (4(2) - 3)) = -2
((3 - 8) / 5) * (10 / (8 - 3)) = -2
(-5 / 5) * (10 / 5) = -2
-1 * (2 / 1) = -2
-1 * 2 = -2
now we take x = 0
((3 - 4x) / 5) * (10 / (4x - 3)) = -2
((3 - 4(0)) / 5) * (10 / (4(0) - 3)) = -2
((3 - 0) / 5) * (10 / (0 - 3)) = -2
(3 / 5) * (10 / -3) = -2
(3 * 10) / (5 * -3) = -2
30 / -15 = -2
2 / -1 = -2
Niels
You are probably more interested in the answer to the x=0 mystery :)
If x cannot be (3/4) then it can be 0, it can also be 2, 3 or (13/2)
WE NEED an actual value for x to calculate the expression.
The solution given in the app takes x=0 but we can take 'every' number for x BUT (3/4).
You already might have noticed that when x is allowed to be 0, often the 0 is taken above all other numbers because 0 will lessen the calculations ergo 20x >>> 20*23 against 20*0, which would you prefer :)
we'll take x = 2
((3 - 4x) / 5) * (10 / (4x - 3)) = -2
((3 - 4(2)) / 5) * (10 / (4(2) - 3)) = -2
((3 - 8) / 5) * (10 / (8 - 3)) = -2
(-5 / 5) * (10 / 5) = -2
-1 * (2 / 1) = -2
-1 * 2 = -2
now we take x = 0
((3 - 4x) / 5) * (10 / (4x - 3)) = -2
((3 - 4(0)) / 5) * (10 / (4(0) - 3)) = -2
((3 - 0) / 5) * (10 / (0 - 3)) = -2
(3 / 5) * (10 / -3) = -2
(3 * 10) / (5 * -3) = -2
30 / -15 = -2
2 / -1 = -2
Niels