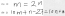Discussion
The ten’s digit of a two-digit number is twice the unit’s digit. Reversing the digits yields a new number that is 27 less than the original number. Which one of the following is the original number?
*This question is included in Nova Math - Problem Set B: Substitution (Plugging in), question #1
| (A) | 12 |
| (B) | ... |
| (C) | ... |
| (D) | ... |
| (E) | ... |
| (F) | ... |
The solution is
Posted: 05/20/2012 11:31
Why wouldn't C be the answer
Posted: 05/20/2012 13:41
C can't be the answer because it doesn't meet the conditions set in the problem. 4 (the ten's digit) is not twice 3 (the unit digit). Whereas 6 is twice 3, and 63 - 27 = 36, the number you get if you switch the ten's and unit's digits. Attached is the way to solve it using equations.
Posted: 10/23/2012 16:55
Here is a walkthrough.
Posted: 11/21/2012 10:45
21y=12y+27 so y=3 (y is the ones digit)
Posted: 04/13/2014 06:23
Could you please explain this question?..
Posted: 04/21/2014 14:05
Ms Qi Gao, please review the discussion thread and open the attachment that contributor Joel Brainer wrote. It has a detailed step-by-step explanation.
Posted: 08/26/2015 09:46
I don't understand
Posted: 08/26/2015 09:48
I'm in Ghana all this seems very difficult
I think I'll need some help
I have an exam this January
I think I'll need some help
I have an exam this January