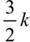Discussion
If 0 < k < 1, then which of the following must be less than k?
| (A) |
|
| (B) | ... |
| (C) | ... |
| (D) | ... |
| (E) | ... |
| (F) | ... |
The solution is
Posted: 01/08/2012 02:08
I'm wondered. What if the number is too complicated, what should I do?
Posted: 01/08/2012 20:31
Jirateep, the strategy to solve this problem is reasoning using the properties in context of their 'new setting', like 25 will always be LARGER than the root of 25, like 25 will always be SMALLER than 25^2
The only possible pitfall here is that numbers smaller than 1 have a different outcome e.g. 0.25 will always be SMALLER than the root of 0.25, like 0.25 will always be LARGER than 0.25^2
So we'll only declare some rules of the number like sign and whether it's greater or smaller than 1 to solve it.
Example:
Which number is largest, when x > 1 and x < 67 or 1 < x < 67
A) 4x
B) 15x
C) (22-19)x
The only calculation we might do is 22-19=3 to see whether it is larger than 15 but it is reason that solved the problem -> its evident. However if the limits given were x < 0 we would have a different outcome but still by reason :)
Niels
The only possible pitfall here is that numbers smaller than 1 have a different outcome e.g. 0.25 will always be SMALLER than the root of 0.25, like 0.25 will always be LARGER than 0.25^2
So we'll only declare some rules of the number like sign and whether it's greater or smaller than 1 to solve it.
Example:
Which number is largest, when x > 1 and x < 67 or 1 < x < 67
A) 4x
B) 15x
C) (22-19)x
The only calculation we might do is 22-19=3 to see whether it is larger than 15 but it is reason that solved the problem -> its evident. However if the limits given were x < 0 we would have a different outcome but still by reason :)
Niels
Posted: 01/17/2012 09:38
Jirateep, that's a good question and thought. You are doing a 2nd degree thinking process, i.e., not only solving the problem at hand, but also abstracting the problem into a type of problem. By thinking that way and actually working out the new problem that you yourself have created, you will be much readier than the typical test taker.
Posted: 01/13/2013 00:36
I don't understand this at all
Posted: 01/13/2013 18:06
Joseph,
If ( k is greater than 0 ) AND ( k is smaller than 1 )
Though the value of k is variable, is has a lower and upper limit thus k is within a certain range, that's why the two rules are contracted as one, a range-expression.
Then which answer has a result smaller than k.
Each of the supplied answers demand that you substitute k for a real value in order to evaluate the expression. The in-app solution takes k=1/4, this is correct since 1/4 is greater than 0 and 1/4 is smaller than 1, however we'll take 3/8 this is correct for the same reasons.
A. (3/2)*k = (3/2)*(3/8) = 9/16
Is k=3/8=6/16 greater than 9/16? Nope
B. 1/k is called the reciprocal, when you exchange the numerator and denominator you have the reciprocal of a fraction however we will calculate it
1/(3/8) = (1/1)/(3/8) remember the rule division of fraction is the same as to multiply with the reciprocal thus (1/1)*(8/3) = 8/3
Is 3/8 greater than 8/3?
Is 9/24 greater than 64/24? Nope.
C. |k|=|3/8|=3/8
This expression means the absolute value of k thus a negative k becomes a positive k and a positive k remain the positive k.
Is 3/8 greater than 3/8? Nope.
D. sqrt(k)=sqrt(3/8)=sqrt(3)/sqrt(8)
Numerator 2*2=4, (3/2)*(3/2)=9/4=2+1/4 thus larger than 3/2
Denominator 3*3=9, (5/2)*(5/2)=25/4=6+1/4 thus larger than 5/2
(3/2)/(5/2)=(3/2)*(2/5)=6/10=2/5 approximate
Is 3/8 greater than 2/5?
Is 15/40 greater than 16/40? Nope.
E. k^2=(3/8)^2=9/64
Is 3/8=24/64 greater than 9/64? Yep.
This is the numerical method, knowing the properties of numbers and processes e.g. fractional multiplication, the more abstract logical method can be used.
Niels
If ( k is greater than 0 ) AND ( k is smaller than 1 )
Though the value of k is variable, is has a lower and upper limit thus k is within a certain range, that's why the two rules are contracted as one, a range-expression.
Then which answer has a result smaller than k.
Each of the supplied answers demand that you substitute k for a real value in order to evaluate the expression. The in-app solution takes k=1/4, this is correct since 1/4 is greater than 0 and 1/4 is smaller than 1, however we'll take 3/8 this is correct for the same reasons.
A. (3/2)*k = (3/2)*(3/8) = 9/16
Is k=3/8=6/16 greater than 9/16? Nope
B. 1/k is called the reciprocal, when you exchange the numerator and denominator you have the reciprocal of a fraction however we will calculate it
1/(3/8) = (1/1)/(3/8) remember the rule division of fraction is the same as to multiply with the reciprocal thus (1/1)*(8/3) = 8/3
Is 3/8 greater than 8/3?
Is 9/24 greater than 64/24? Nope.
C. |k|=|3/8|=3/8
This expression means the absolute value of k thus a negative k becomes a positive k and a positive k remain the positive k.
Is 3/8 greater than 3/8? Nope.
D. sqrt(k)=sqrt(3/8)=sqrt(3)/sqrt(8)
Numerator 2*2=4, (3/2)*(3/2)=9/4=2+1/4 thus larger than 3/2
Denominator 3*3=9, (5/2)*(5/2)=25/4=6+1/4 thus larger than 5/2
(3/2)/(5/2)=(3/2)*(2/5)=6/10=2/5 approximate
Is 3/8 greater than 2/5?
Is 15/40 greater than 16/40? Nope.
E. k^2=(3/8)^2=9/64
Is 3/8=24/64 greater than 9/64? Yep.
This is the numerical method, knowing the properties of numbers and processes e.g. fractional multiplication, the more abstract logical method can be used.
Niels
Posted: 01/25/2013 19:29
How was I suppose to know to use 1/4? Am I just supposed to plug anything in?
Posted: 05/28/2013 18:09
I don't understand how k(k) (k^2) can be less than k itself. If it is multiplied by itself, clearly it's more than what it was. I just don't get it.
Posted: 05/28/2013 18:31
Andres, for example, when k is a fraction.