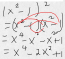Discussion
| (A) |  |
| (B) | ... |
| (C) | ... |
| (D) | ... |
| (E) | ... |
| (F) | ... |
The solution is
Posted: 12/27/2011 19:10
Please explain i don't get how to do the exponent in a negative # like -2. 4<~ exponent
Posted: 12/28/2011 15:09
Arcelia. -2^4 = - (2x2x2x2) = -16; whereas (-2)^4 = (-2 x -2 x -2 x -2) =16. Do you see the difference? Power or exponent has a higher priority over the subtraction or negation operator. To make the - higher priority, you need to put it in parentheses.
So, (x^2 - 1)^2 = x^4 -2x^2 +1. Negating the whole thing, we get: -x^4 + 2x^2 -1. Adding -16 we get -x^4 + 2x^2 -17, which is C.
So, (x^2 - 1)^2 = x^4 -2x^2 +1. Negating the whole thing, we get: -x^4 + 2x^2 -1. Adding -16 we get -x^4 + 2x^2 -17, which is C.
Posted: 12/28/2011 15:21
Video explanation of the solution.
Posted: 02/27/2012 22:58
Where does the -2x^2 come from??
Posted: 02/27/2012 23:23
Gina, see the attached explanation. -2x^2 comes from foiling (x^2 -1)^2
Posted: 02/27/2012 23:25
Gina, This is the attachment to previous post.
Posted: 03/08/2012 22:54
Why do you use the FOIL method?
Posted: 03/09/2012 01:30
Gina, please see the attachment of the previous post. Foiling is used when you multiply one bracketed term with another bracketed term. Squaring a bracketed term is the same as multiplying it by itself.
Posted: 04/21/2012 23:47
I thought that every negative number at any exponent was going to equal to a positive number? Or is that only applies to negative exponents???
Posted: 04/22/2012 00:25
Got it
Posted: 05/11/2014 05:10
Hi Joel. I did not understand where the 2x^2 came from. Thank you, Vini.
Posted: 05/12/2014 15:26
Hi, Vini, Joel is on a break. But to answer your question: in the equation, we have this factor:
(x^2 – 1)^2, which is simply (x^2-1)(x^2 – 1), and so using the distributive property you multiple x^2 with x^2, -1 with x^2, x^2 with -1, and finally -1 with -1, to get:
(x^4 – 2x^2 + 1).
You may want to review your algebra notes. For example, this site: http://www.purplemath.com/modules/polymult.htm
(x^2 – 1)^2, which is simply (x^2-1)(x^2 – 1), and so using the distributive property you multiple x^2 with x^2, -1 with x^2, x^2 with -1, and finally -1 with -1, to get:
(x^4 – 2x^2 + 1).
You may want to review your algebra notes. For example, this site: http://www.purplemath.com/modules/polymult.htm