Discussion
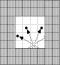
In the game of chess, the Knight can make any of the moves displayed in the diagram to the right. If a Knight is the only piece on the board, what is the greatest number of spaces from which not all 8 moves are possible?
*This question is included in Nova Math - Problem Set M: Elimination Strategies, question #6
| (A) | 8 |
| (B) | ... |
| (C) | ... |
| (D) | ... |
| (E) | ... |
| (F) | ... |
The solution is
Posted: 01/03/2015 09:53
What does this question mean? I don't understand at all.
Posted: 12/12/2015 11:55
same here. Can someone further explain the question asked?
Posted: 12/12/2015 12:33
Hi Joelene,
In the attached graphic, the shaded squares represent the areas from which not all 8 moves are possible (there are 48 shaded squares).
Note: Each valid move for the Knight consists of moving through either two horizontal squares and then one vertical square or two vertical squares and then one vertical horizontal square. Doing this from any of the shaded squares would move the Knight off the board.
Nova Press
In the attached graphic, the shaded squares represent the areas from which not all 8 moves are possible (there are 48 shaded squares).
Note: Each valid move for the Knight consists of moving through either two horizontal squares and then one vertical square or two vertical squares and then one vertical horizontal square. Doing this from any of the shaded squares would move the Knight off the board.
Nova Press