For all real numbers a and b, where a · b ≠ 0, let . Then which ... ...
Replies to This Thread: 0
|
----
Posted: 01/15/2013 20:53
Is there any way you can create different A,B,C options when you must choose more than one? Similar to the oval and square type options on the actual GRE.
Contributor
Replies to This Thread: 0
|
----
Posted: 01/15/2013 21:09
This is a great suggestion. Thanks!
Replies to This Thread: 1
|
----
For all real numbers a and b, where a · b ≠ 0, let . Then which ... ...
Posted: 06/02/2013 09:42
Can you explain this problem
Admin
Reply 1 of 1
Replies to This Thread: 0
|
----
Posted: 06/06/2013 23:12
Petit, in defined function questions, where you see different symbols that♢ define a function, it is useful to think of ƒ(x), which is what you normally see in typical math classes.
Hence, think of a♢b = ƒ(a,b), which here is defined as a*b - a/b.
b♢a, then, would be f(b,a) = b*a - b/a. Similarly, a♢a = a*a - a/a = a^2 - 1.
Now, you should be able to apply this knowledge and work out answers A, B, and C, and see which ones hold true.
Hope this helps.
Replies to This Thread: 1
|
----
For all real numbers a and b, where a · b ≠ 0, let . Then which ... ...
Posted: 04/22/2014 11:11
Sorry, but I still don't see the connection of how choice b and c relate to the original
Equation.
Admin
Reply 1 of 1
Replies to This Thread: 0
|
----
Posted: 04/28/2014 16:27
Ronnie, I will repeat my prior explanation.
In defined function questions, where you see different symbols such as ♢ that define a function, it is useful to think of the symbol as forming ƒ(x), which is what you normally think of when you hear the word "function".
Hence, think of a♢b = ƒ(a,b), which here is defined as a*b - a/b.
b♢a, then, would be f(b,a) = b*a - b/a. Similarly, a♢a = a*a - a/a = a^2 - 1.
Now, you should be able to apply this knowledge and work out answers A, B, and C, and see which ones hold true.
Hope this helps.
Replies to This Thread: 0
|
----
For all real numbers a and b, where a · b ≠ 0, let . Then which ... ...
Posted: 04/22/2014 11:11
Sorry, but I still don't see the connection of how choice b and c relate to the original
Equation.
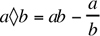. Then which of the following must be true?
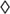b = b
