Let . For what value of x does for all values of y?
Replies to This Thread: 1
|
----
Let . For what value of x does for all values of y?
Posted: 10/21/2013 17:00
Confused on how A is the answer
Contributor
Reply 1 of 1
Replies to This Thread: 0
|
----
Posted: 10/29/2013 17:22
Hi Meru, have you tried to follow the explanation? If you are still confused please post again.
Replies to This Thread: 1
|
----
Let . For what value of x does for all values of y?
Posted: 10/31/2013 19:13
I didn't get it, it's so confusing...
Contributor
Reply 1 of 1
Replies to This Thread: 2
|
Hide
Posted: 11/01/2013 14:15
Hello Jayden, and also Meru.
Here, x⊝y is defined as x√y - y - 2x. We are asked, what values of x will set x⊝y = -y?
So all we have to do is set x√y - y - 2x = -y, and solve for x.
x√y - y - 2x = -y;
x√y - 2x = 0, then through associative property: x(√y -2) = 0
In order for that last equation to be true regardless of what y is, x has to be 0. So A is the answer.
Reply 1 of 2
Replies to This Thread: 0
|
----
Posted: 04/17/2014 17:00
What if x=0? It's still equal 0
Admin
Reply 2 of 2
Replies to This Thread: 0
|
----
Posted: 04/21/2014 13:45
Yini, exactly the point. If x=0, then regardless of what y is, x (√y - 2) will be = 0. So, if x = 0, x⊝y = -y, regardless of what y is.
Replies to This Thread: 0
|
----
Let . For what value of x does for all values of y?
Posted: 04/13/2014 22:57
I think E is the correct answer.
Replies to This Thread: 1
|
----
Let . For what value of x does for all values of y?
Posted: 04/17/2014 16:59
what if x equal 0? Then, x(/y-2) still equal 0, so I think the answer is E
Admin
Reply 1 of 1
Replies to This Thread: 0
|
----
Posted: 04/21/2014 13:46
Yini, please see the explanation by Joel Brainer in the discussion thread. We are looking for a value of x that will make the equation x⊝y = -y true regardless of the value of y.
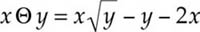. For what value of x does 
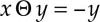for all values of y?
