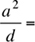If a = 3b, b2 = 2c, 9c = d, then
Replies to This Thread: 0
|
----
Posted: 05/10/2012 02:01
I don't understand this particular question can some explain how they got this answer.

Contributor
Replies to This Thread: 0
|
----
Posted: 05/10/2012 02:17
Teesha, this is a case of substitution. Since we are trying to solve for a^2 / d, we gotta find ways to express a and d using common variables, so that we can cancel them in the numerator and the denominator, eventually.
Starting with a:
a = 3b
a^2 = 9b^2
Wait, we are told that b^2 = 2c
So, a^2 = 9 x 2c = 18c
Let's express d in terms of c
d = 9c
Since both numerator and denominator are now expressed in terms of c, we can solve:
a^2 / d = 18c / 9c = ...
Replies to This Thread: 0
|
----
Posted: 07/04/2012 06:55
So, the solution makes perfect sense when it's laid out this way. I understood perfectly that this would be a "simple" process of substitution, but my trouble comes in knowing how to start the substitution process. I started differently and ended up with an equation that made no sense at all.

Contributor
Replies to This Thread: 0
|
----
Posted: 07/04/2012 11:06
Andrew, there are 4 variables a, b, c, and d. Since the term in question is expressed in a and d, we have a choice to substitute b or c for a and d. But we have to eventually express everything in b or c.
Replies to This Thread: 0
|
----
Posted: 08/18/2012 12:42
How was the 'b' canceled? I got the correct answer but...

Admin
Replies to This Thread: 0
|
----
Posted: 08/18/2012 23:19
P L, please look up the thread. This problem was answered and explained pretty well.
Replies to This Thread: 0
|
----
If a = 3b, b2 = 2c, 9c = d, then
Posted: 07/20/2013 10:04
I will go with picking numbers strategy for those kind of questions, lets assume B = 1, then A = 3, C = 1/2, d = 4.5
So 3^2/4.5 = 9/4.5 = 2